Travelling Salesman Problem (TSP)

Travelling Salesman Problem (TSP) merupakan salah satu permasalahan optimasi klasik yang sulit untuk dipecahkansecara konvensional. Penyelesaian eksak terhadap persoalanini akan melibatkan algoritma yang mengharuskan mencarikemungkinan semua solusi yang ada [1]. Sehingga akanterjadi ledakan kombinasi dan membuat kompleksitas waktudari eksekusi algoritma sangat tinggi.

Masalah TSP melibatkan seorang sales yang harus melakukan kunjungan ke sejumlah kota dalam menjajakan produknya. Rangkaian kota-kota yang dikunjungi harusmembentuk suatu jalur sedemikian sehingga kota-kotatersebut hanya boleh dilewati tepat satu kali dan kemudiankembali lagi ke kota awal.

Kasus seperti ini sering diistilahkandengan sirkuit hamilton, representasinya dikenal dengan istilah hamiltonian. Penyelesaian terhadap permasalahanTSP ini adalah untuk memperoleh jalur terpendek. Penyelesaian eksak terhadap masalah TSP mengharuskan untuk melakukan perhitungan terhadap semua kemungkinan rute yang dapat diperoleh, kemudian memilih salah satu rute yang terpendek. Untuk itu jika terdapat  n  kota yang harusdikunjungi, maka terdapat n! kombinasi kota yang akandi bandingkan jarak masing-masing. Dengan cara ini waktu komputasi yang dibutuhkan akan jauh meningkat seiring dengan bertambahnya jumlah kota yang harus dikunjungi.

Di dalam algoritma greedy prinsip Pencarian jalurter pendek memakai fungsi seleksi dan itu sangat berguna untuk menentukan jalan tersingkat untuk menuju suatu tempat sesuai dengan asumsi diatas. Dalam penerapannya, algoritma ini tidak selalu mendapatkan solusi optimal namun pasti menemukan solusi. Kelebihan algoritma ini adalah kemampuannya menemukan solusi dengan jumlah node yang banyak dilakukan dengan sangat cepat. Algoritma greedy biasanya digunakan untuk menentukan memecahkan masalah lintasan linier dimana asal dan tujuan merupakan node yang berbeda. Hal ini menjadi kendala apabila diterapkan pada kasus TSP, dimana jalur yang ada merupakan jalur hamiltonian. Hal ini dapat diatasi dengan menggunakan penanda.

Penanda

TSP merupakan jalur Hamiltonian, sehingga setiap node dimungkinkan memiliki dua arah. Jika kita menggunakan algoritma greedy pada kasus ini, maka harus dilengkapi dengan kemampuan untuk mengenali kota yang telah dilewati agar tidak terjadi perulangan. Dengan kata lain, satu kota hanya dikunjungi sekali. Untuk menyelesaikan hal tersebut, dibutuhkan sebuah penanda setiap kota yang telah dikunjungi. Kota atau node yang telah dikunjungi harus ditandai,  misalnya inisialisasi setiap kota mempunya tanda = 0, jika kota telah dikunjungi, maka tandanya berubah menjadi 1. Ketika proses pelacakan jalur terjadi, kota dengan tanda = 1 tidak perlu dilewati/diproses. Dengan adanya penanda pada algoritma greedy, proses pelacakan dapat dilakukan tanpa ada kota yang dikunjungi berulang. Hal ini memudahkan pelacakan untuk kembali kekota asal.

Kompleksitas Algoritma

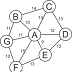
Untuk memudahkan menghitung kompleksitas algoritma greedy dengan penanda, berikut diberikan contoh lintasan TSP beserta costnya. Misalnya terdapat 4 kota yaitu ABCDE, dimana jarak A ke B = 7, A ke C = 3, A ke D = 4, B ke C = 5,B ke D = 8 dan C ke D = 2. Grafnya dapat dilihat dibawah ini.

           Graf TSP dengan empat node

Proses pelacakan / penentuan lintasan sesuai dengan pseudocode dapat digambarkan dalam bentuk tree seperti berikut:

Contoh Pelacakan dalam bentuk tree

 Dari Gambar, ditemukan solusi jalur terpendek adalah A-C-D-B-A dengan total cost   adalah 20. Kompleksitas yang terjadi pada contoh diatas untuk mendapatkan solusi sebanyak7 rute, yaitu A-B, A-C, A-D, C-B, C-D, D-B dan B-A. Dengan cara yang sama, jika terdapat 3 node, makadi peroleh kompleksitas sebanyak 4 rute, 5 node, kompleksitasnya adalah 11, 10 node, kompleksitasnya adalah 46. Hal tersebut membentuk sebuah pola sehingga dapat disimpulkan bahwa untuk menghitung kompleksitas Algoritma Greedy dengan penanda dalam menyelesaikan TSP, jika diinput n kota, maka akan terjadi (n(n-1)/2)+1.

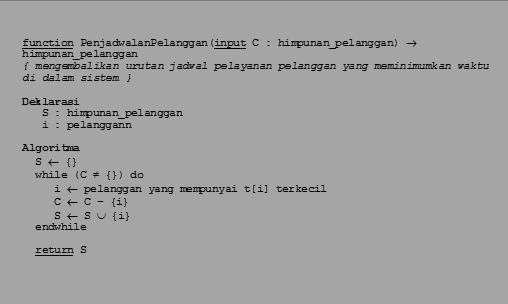
Pseudo Code

Ide sederhana untuk membuat pseudo codenya adalahsebagai berikut :

1.         Input jumlah node

2.         Input jarak antar kota, dimana jarak yang diinputcukup sekali, misalnya cukup menginput jarak antarakota A ke kota B, secara otomatis, program akanmengisi jarak antara kota B ke kota A.

3.         Setiap yang telah dilewati diberi penanda = 1,sementara kota yang belum dilewati secara defaultmempunyai penanda = 0.

4.         Gunakan algoritma greedy untuk mencari optimumlocal step by step dengan tidak memproses kota yangtelah dilewati (yaitu ditandai dengan penanda=1).

5.         Outpunya berupa jalur optimal sesuai prinsip greedydan total cost yang dibutuhkan.

Pseudo code untuk aplikasi pemecahan TSP mengunakanalgoritma greedy dengan penanda sebagai berikut:

Dengan menginput jumlah node (n) dan jarak antar kota (cost[i,j]) pseudo code diatas akan menghasilkan jalur optimal(Lintasan) beserta total jarak yang dibutuhkan (cost) sesuai prinsip greedy.

Penjadwalan Pelanggan

      2.      Minimisasi Waktu di dalam Sistem (Penjadwalan)

      Persoalan: Sebuah server (dapat berupa processor, pompa, kasir di bank, dll) mempunai n                     pelanggan (customer, client) yang harus dilayani. Waktu pelayanan untuk setiap pelanggan 

      i  adalah ti.

            Minimumkan total waktu di dalam sistem: 

       (waktu di dalam sistem)

Ekivalen dengan meminimumkan waktu rata-rata pelanggan di dalam sistem.

Misal :  Tiga pelanggan dengan

            t1 = 5,  t2 = 10,            t3 = 3,

Enam urutan pelayanan yang mungkin:

============================================

Urutan             T 

============================================                                               

1, 2, 3: 5 + (5 + 10) + (5 + 10 + 3 ) = 38

1, 3, 2:             5 + (5 + 3) + (5 + 3 + 10) = 31

2, 1, 3: 10 + (10 + 5) + (10 + 5 + 3) = 43

2, 3, 1: 10 + (10 + 3) + (10 + 3 + 5) = 41

3, 1, 2: 3 + (3 + 5) + (3 + 5 + 10) = 29 ¬ (optimal)

3, 2, 1: 3 + (3 + 10) + (3 + 10 + 5) = 34

============================================

Exhaustive Search

·         Urutan pelangan yang dilayani oleh server merupakan suatu permutasi

·         Jika ada n orang pelanggan, maka tedapat n! urutan pelanggan

·         Untuk mengevaluasi fungsi obyektif : O(n)

·         Kompleksitas algoritma exhaustive search = O(nn!)

Penyelesaian dengan algoritma greedy

                   ·     Strategi greedy: Pada setiap langkah, pilih pelanggan yang membutuhkan waktu                                   pelayanan terkecil di antara pelanggan lain yang belum dilayani.

·         Agar proses pemilihan pelanggan berikutnya optimal, urutkan pelanggan berdasarkan  waktu pelayanan dalam urutan yang menaik.

·     Jika pelanggan sudah terurut, kompleksitas algoritma greedy = O(n).

·         Algoritma greedy untuk penjadwalan pelanggan akan selalu menghasilkan solusi optimum.

·         Teorema. Jika t1 £ t2 £ … £ tn maka pengurutan  ij = j,  1 £ j £ n meminimumkan

                      

                         

       untuk semua kemungkinan permutasi ij. 

Referensi :

        http://topaninfo.blogspot.co.id/2012/12/Algoritma-GREEDY-Definisi-Contoh-                       Program.html

        https://www.it-jurnal.com/pengertian-algoritma-greedy/

        https://bertzzie.com/knowledge/analisis-algoritma/Greedy.html#algoritma-greedy

        http://kurniadi-addi.blogspot.co.id/2015/07/materi-analisis-algortima-algoritma.html

Penukaran Uang

    1.      Kasus Penukaran Uang : Diberikan uang senilai A = 8 $. Tukar A dengan koin-koin uang yang             tersedia banyak koin 1 $, 3 $, 5 $. Berapa jumlah minimum koin yang diperlukan untuk penukaran      tersebut?

 Penyelesaian :

·         Persoalan Optimasi

8 = 1+1+1+1+1+1+1+1 (8 koin)

8 = 1+1+1+5  (4 Koin)

8 = 1+1+3+3 (4 koin)

8 = 5+3  (2 koin)

Banyak koin minimum yang dapat ditukar untuk menghasilkan 8 $ adalah :

Minimum : 1 koin 5$, 1 koin 3$

Jadi : solusi optimal 2 koin

·         Exhaustive –Search

Untuk mencari kompleksitas hitung jumlah koin dengan nilai yang berbeda,

Misal :

1+1+1+1+1+1+1+1 = 8  ( jumlah nilai koin berbeda ada 1)

1+1+1+5 = ( jumlah nilai koin berbeda ada 2 )

3+5 = 8  ( jumlah nilai koin berbeda ada 2 )

Maka : pilih jumlah nilai koin yang berbedanya paling sedikit. 

Jadi di dapat 2 buah koin.

Untuk 2 buah koin terdapat berapa kemungkinan . . . ?

Misal : 1 buah koin terdapat angka dan gambar.

Maka kemungkinan yang bisa terjadi adalah :

{A,A} {A,G} {G,G} {G,A}

Untuk 2 koin ada --> 4    kemungkinan

Untuk 3 koin ada --> 8 kemungkinan

Untuk  n  koin ada à  2ⁿ  kemungkinan

Untuk mengevaluasi setiap kemungkinan dibutuhkan n eksekusi.

Maka, kompleksitas : n * 2ⁿ

                      Pseudo-code Penukaran Uang

                Referensi :

•         http://topaninfo.blogspot.co.id/2012/12/Algoritma-GREEDY-Definisi-Contoh-Program.html
•         https://www.it-jurnal.com/pengertian-algoritma-greedy/
•         https://bertzzie.com/knowledge/analisis-algoritma/Greedy.html#algoritma-greedy
•         http://kurniadi-addi.blogspot.co.id/2015/07/materi-analisis-algortima-algoritma.html

ALGORITMA GREEDY

Secara Harfiah Greedy artinya rakus atau tamak, sifat yang berkonotasi negatif. Orang yang memiliki sifat ini akan mengambil sebanayak mungkin atau mengambil yang paling bagus atau yang paling mahal. Sesuai dengan arti tersebut, Prinsip Greedy adalah take what you can get now. Dalam kehidupan sehari hari Greedy dapat digunakan dalam masalah seperti :

1.      Memilih beberapa jenis investasi.

2.      Mencari jalur tersingkat dari Bandung ke Surabaya.

3.      Memilih jurusan di Perguruan Tinggi

4.      Bermain Kartu Remi

5.      Memilih spesifikasi komputer yang terbaik dengan budget maksimum tertentu.

1.1          Definisi Algoritma Greedy

Algoritma greedy adalah langkah per langkah dalam mencari solusi atas sebuah masalah. Terdapat banyak pilihan yang perlu dieksplorasi pada setiap langkah solusi. Oleh karena itu, pada setiap langkah harus dibuat keputusan yang terbaik dalam menentukan pilihan. Keputusan yang telah diambil pada suatu langkah tidak dapat diubah lagi pada langkah selanjutnya. Algoritma greedy merupakan salah satu dari sekian banyak algoritma yang sering di pakai dalam implementasi sebuah system atau program yang menyangkut mengenai pencarian “optimasi”.

1.2          Personal Optimasi

Persoalan Optimasi adalah persoalan yang tidak hanya mencari sekedar solusi, tetapi mencari solusi terbaik. Dalam kehidupan sehari hari, banyak terdapat persoalan yang menuntut pencarian solusi optimum. Persoalan tersebut dinamakan persoalan optimasi(optimization Problems).

Persoalan optimasi ada dua macam :

        ·         Maksimasi (maximization)

        ·         Minimasi (minimization)

Contoh Persoalan Optimasi :

( Masalah Penukaran Uang): Diberikan uang senilai A = 32. Tukar A dengan koin-koin uang yang tersedia banyak koin 1, 5, 10, 25. Berapa jumlah minimum koin yang diperlukan untuk penukaran tersebut?

              ·         Uang senilai A = 32 dapat ditukar dengan banyak cara berikut:

                  32 = 1 + 1 + … + 1                                        (32 koin)

                  32 = 5 + 5 + 5 + 5 + 10 + 1 + 1                     (7 koin)

                  32 = 10 + 10 + 10 + 1 + 1                             (5 koin)

                  … dst                  

              ·         Minimum: 32 = 25 + 5 + 1 + 1       (4 koin)

1.3          Solusi Optimasi

Solusi optimum adalah solusi yang bernilai minimum atau maksimum dari sekumpulan alternatif solusi yang mungkin.

1.4          Skema Umum Algoritma Greedy

Elemen-elemen algoritma greedy :

       1.     Himpunan kandidat, C

       Berisi elemen-elemen pembentuk solusi.

       2.     Himpunan solusi, S

       Berisi kandidat-kandidat yang terpilih sebagai solusi persoalan.

       3.      Fungsi seleksi (selection function)

       Memilih kandidat yang paling memungkinkan mencapai solusi optimal. Kandidat yang sudah              dipilih pada suatu langkah tidak pernah dipertimbangkan lagi pada langkah selanjutnya.

       4.      Fungsi kelayakan (feasible)

      Memeriksa apakah suatu kandidat yang telah dipilih dapat memberikan solusi yang layak, yakni         kandidat tersebut bersama-sama dengan himpunan solusi yang sudah terbentuk tidak melanggar         kendala (constraints) yang ada. Kandidat yang layak dimasukkan ke dalam himpunan solusi,                sedangkan kandidat yang tidak layak dibuang dan tidak pernah dipertimbangkan lagi.

       5.      Fungsi obyektif

       Fungsi objektif yaitu fungsi yang memaksimumkan atau meminimumkan nilai solusi(misalnya            panjang lintasan, keuntungan, dan lain-lain).

      Contoh :

       Pada masalah penukaran uang:

a.       Himpunan kandidat, C : Himpunan koin yang merepresentasikan nilai 1, 5, 10, 25, paling sedikit mengandung satu koin untuk setiap nilai.

b.      Himpunan solusi, S : Total nilai koin yang dipilih tepat sama jumlahnya dengan nilai uang yang ditukarkan.

c.       Fungsi seleksi: Pilihlah koin yang bernilai tertinggi dari himpunan kandidat yang tersisa.

d.      Fungsi layak : Memeriksa apakah nilai total dari himpunan koin yang dipilih tidak melebihi jumlah uang yang harus dibayar.

e.       Fungsi obyektif: Jumlah koin yang digunakan minimum.

 

1.5          Skema Umum Algoritma Greedy Dalam Notasi Algoritma

             Skema Algoritma dapat dirumuskan sebagai berikut :

                                                   i.            Inisialisasi S dengan nilai kosong.

                                                  ii.            Pilih sebuah kandidat (dengan fungsi SELEKSI) dari C

                                                  iii.          Kurangi C dengan kandidat yang sudah dipilih dari langkah ii

                                                  iv.           Periksa apakah kandidat yang dipilih bersama” himpunan solusi membentuk solusi 

                                   yang layak (diperiksa oleh Fungsi FEASIBLE).

               Jika YA à masukkan kandidat ke himpunan solusi ,

               TIDAK à buang kandidat

                                                    v.            Periksa apakah himpunan solusi sudah memberikan solusi lengkap (dengan fungsi 

                                   SOLUSI)

               Jika YA à berhenti ,

               TIDAK à ulangi langkah ii

Skema umum algoritma greedy dalam pscedu-code :

        ·         Pada akhir setiap lelaran, solusi yang terbentuk adalah optimum lokal.

        ·         Pada akhir dikalangan while-do diperoleh optimum global.

        Referensi :

•         http://topaninfo.blogspot.co.id/2012/12/Algoritma-GREEDY-Definisi-Contoh-Program.html
•         https://www.it-jurnal.com/pengertian-algoritma-greedy/
•         https://bertzzie.com/knowledge/analisis-algoritma/Greedy.html#algoritma-greedy
•         http://kurniadi-addi.blogspot.co.id/2015/07/materi-analisis-algortima-algoritma.html
•