1. Diberikan bilangan bulat a1, a2, . ., an (tidak ada elemen ganda
dan sudah terurut menaik). Hitunglah kompleksitas waktu Terbaik( Tmin(n)),
Terburuk(Tmax(n)), dan Rata-rata(Tavg(n)) dari algoritma
mencari elemen minimum larik dibawah ini.
Penyelesaian :
a.
Kasus Terbaik (T
min(n))
Adalah bila operasi perbandingan (a1 <
min) yang dilakukan satu kali,
sehingga :
Tmin(n) = 1.
b.
Kasus Terburuk
(T max(n))
Adalah bila nilai min ada pada larik terakhir.
T
max(n) = n
c.
Kasus Rata-rata
T avg(n)
T avg(n) =
2. Diberikan bilangan bulat a1, a2, . ., an (tidak ada elemen ganda
dan sudah terurut menaik). Hitunglah kompleksitas waktu Terbaik( Tmin(n)),
Terburuk(Tmax(n)), dan Rata-rata(Tavg(n)) dari algoritma
pencarian biner dibawah ini menghasilkan
indeks elemen yang bernilai sama dengan x, jika x tidak ditemukan, maka indeks
0 akan dihasilkan.
Penyelesaian :
a.
Kasus Terbaik (T
min(n))
Adalah bila x ditemukan pada elemen
pertengahan (amid ) , dan operasi perbandingan elemen (amid
= x ) yang dilakukan hanya satu kali,
sehingga :
Tmin(n) = 1.
b.
Kasus Terburuk
(T max(n))
Adalah elemen x ditemukan ketika ukuran
larik = 1. Pada kasus terburuk ini ukuran larik setiap kali memasuki while-do
adalah n, n/2, n/4, n/8, . . ., 1(
sebanyak 2log n kali).
Sehingga :
T
max(n) = 2log n
c.
Kasus Rata-rata
T avg(n)
Kompleksitas waktu rata-rata T avg(n) algoritma Binery Search lebih sulit
ditentukan.
3. Diberikan A larik (tidak ada elemen ganda
dan sudah terurut menaik). Hitunglah kompleksitas waktu Terbaik( Tmin(n)),
Terburuk(Tmax(n)), dan Rata-rata(Tavg(n)) dari algoritma
penyisispan elemen baru x ke larik yang sudah terurut dibawah ini. Algoritma sisip x dibawah ini menghasilkan x
yang sudah disisipkan didalam larik.
Penyelesaian
:
a.
Kasus Terbaik (T
min(n))
Adalah bila x ditemukan pada elemen pertama
A[i] dan operasi perbandingan elemen ( x
< A[i] ) yang dilakukan hanya 1 kali. Sehingga :
Tmin(n) = 1.
b.
Kasus Terburuk
(T max(n))
Adalah elemen x ditemukan pada elemen
larik terakhir A[i] dan operasi perbandingan dilakukan sebanyak n buah. Sehingga :
T
max(n) = n
c.
Kasus Rata-rata
T avg(n)
4. Diberikan
bilangan bulat c1, c2,
. ., cn (tidak ada
elemen ganda). Hitunglah kompleksitas waktu Terbaik( Tmin(n)),
Terburuk(Tmax(n)), dan Rata-rata(Tavg(n)) dari algoritma hitung
jumalah muncul angka 1 dibawah ini
menghasilkan banyaknya jumlah angka 1 dalam larik.
penyelesaian :
a.
Kasus Terbaik (T
min(n))
Tmin(n) = n
Karena semua elemen Ci akan
dibandingkan apakah sama dengan 1 ( Ci = 1 )
b.
Kasus Terburuk
(T max(n))
T
max(n) = n
c.
Kasus Rata-rata
T avg(n))
T avg(n) = n
5. Diberikan
larik L (tidak
ada elemen ganda). Hitunglah kompleksitas waktu Terbaik( Tmin(n)),
Terburuk(Tmax(n)), dan Rata-rata(Tavg(n)) dari algoritma Bubble
Sort dibawah ini.
Penyelesaian
:
a.
Kasus Terbaik (T
min(n))
Data
yang akan disorting telah terurut sebelumnya, sehingga proses perbandingan
hanya dilakukan sebanyak (n-1) kali, dengan satu kali pass. Proses perbandingan
dilakukan hanya untuk memverifikasi keurutan data. Contoh Best-Case dapat dilihat
pada pengurutan data “1 2 3 4” di bawah ini.
Pass
Pertama
(1
2 3 4) menjadi (1 2 3 4)
(1
2 3 4) menjadi (1 2 3 4)
(1
2 3 4) menjadi (1 2 3 4)
Dari
proses di atas, dapat dilihat bahwa tidak terjadi penukaran posisi satu
kalipun, sehingga tidak dilakukan pass selanjutnya. Perbandingan elemen
dilakukan sebanyak tiga kali. Sehingga :
Tmin(n) = n - 1.
b.
Kasus Terburuk
(T max(n))
Data terkecil berada pada ujung array.
Contoh : kasus terburuk dapat dilihat pada
pengurutan data “ 4,3,2,1” dibawah ini.
Pass
Pertama
(4
3 2 1) menjadi (3 4 2 1)
(3
4 2 1) menjadi (3 2 4 1)
(3
2 4 1) menjadi (3 2 1 4)
Pass
Kedua
(3
2 1 4) menjadi (2 3 1 4)
(2
3 1 4) menjadi (2 1 3 4)
(2
1 3 4) menjadi (2 1 3 4)
Pass
Ketiga
(2
1 3 4) menjadi (1 2 3 4)
(1
2 3 4) menjadi (1 2 3 4)
(1
2 3 4) menjadi (1 2 3 4)
Pass
Keempat
(1
2 3 4) menjadi (1 2 3 4)
(1
2 3 4) menjadi (1 2 3 4)
(1
2 3 4) menjadi (1 2 3 4)
Dari
langkah pengurutan di atas, terlihat bahwa setiap kali melakukan satu pass,
data terkecil akan bergeser ke arah awal sebanyak satu step. Dengan kata lain,
untuk menggeser data terkecil dari urutan keempat menuju urutan pertama,
dibutuhkan pass sebanyak tiga kali, ditambah satu kali pass untuk
memverifikasi. Sehingga jumlah proses pada kasus terburuk dapat dirumuskan sebagai
berikut. Sehingga :
T
max(n) = n2
c.
Kasus Rata-rata
T avg(n)
Pada
kondisi average-case, jumlah pass ditentukan dari elemen mana yang mengalami enggeseran ke kiri paling banyak. Hal ini
dapat ditunjukkan oleh proses pengurutan suatu array, misalkan saja (1 8 6 2).
Dari (1 8 6 2), dapat dilihat bahwa yang akan mengalami proses penggeseran paling banyak adalah elemen
2, yaitu sebanyak dua kali.
Pass
Pertama
(1 8 6
2) menjadi (1 8 6 2)
(1 8 6 2)
menjadi (1 6 8 2)
(1 6 8
2) menjadi (1 6 2 8)
Pass
Kedua
(1 6 2
8) menjadi (1 6 2 8)
(1 6 2 8)
menjadi (1 2 6 8)
(1 2 6
8) menjadi (1 2 6 8)
Pass
Ketiga
(1 2 6
8) menjadi (1 2 6 8)
(1 2 6 8)
menjadi (1 2 6 8)
(1 2 6
8) menjadi (1 2 6 8)
Dari
proses pengurutan di atas, dapat dilihat bahwa untuk mengurutkan diperlukan dua
uah passing, ditambah satu buah passing untuk
memverifikasi. Dengan kata lain, jumlah roses
perbandingan dapat dihitung sebagai berikut.
T
avg(n) = n2
Sumber :
- informatika.stei.itb.ac.id/~rinaldi.munir/Matdis/2009.../MakalahStrukdis0910-032.pdf
- Munir, Renaldi. (2011). Algoritma & Pemrogramman Dalam Bahasa Pascal dan C. (edisi revisi). Bandung ; INFORMATIKA.



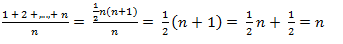








0 komentar:
Posting Komentar