2. Minimisasi Waktu di dalam Sistem (Penjadwalan)
Persoalan:
Sebuah server (dapat berupa processor, pompa, kasir di bank, dll) mempunai n pelanggan (customer, client) yang harus dilayani. Waktu pelayanan untuk setiap
pelanggan
i adalah ti.
Minimumkan total waktu di dalam
sistem:
Ekivalen dengan meminimumkan waktu rata-rata
pelanggan di dalam sistem.
Misal
: Tiga pelanggan dengan
t1 = 5, t2 = 10, t3 = 3,
Enam
urutan pelayanan yang mungkin:
============================================
Urutan T
============================================
1,
2, 3: 5 + (5 + 10) + (5 + 10 + 3 ) = 38
1,
3, 2: 5 + (5 + 3) + (5 + 3 +
10) = 31
2,
1, 3: 10 + (10 + 5) + (10 + 5 + 3) = 43
2,
3, 1: 10 + (10 + 3) + (10 + 3 + 5) = 41
3,
1, 2: 3 + (3 + 5) + (3 + 5 + 10) = 29 ¬ (optimal)
3,
2, 1: 3 + (3 + 10) + (3 + 10 + 5) = 34
============================================
Exhaustive Search
·
Urutan pelangan
yang dilayani oleh server merupakan suatu permutasi
·
Jika ada n orang
pelanggan, maka tedapat n! urutan pelanggan
·
Untuk
mengevaluasi fungsi obyektif : O(n)
·
Kompleksitas
algoritma exhaustive search = O(nn!)
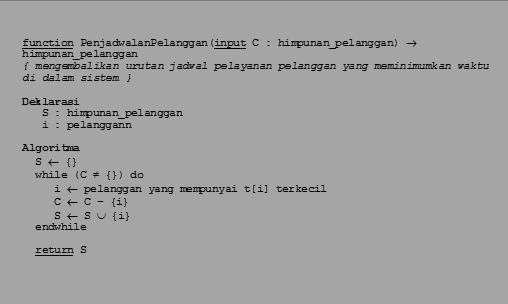
Penyelesaian dengan algoritma greedy
· Strategi greedy: Pada setiap langkah, pilih pelanggan yang membutuhkan
waktu pelayanan terkecil di antara pelanggan lain yang belum dilayani.
·
Agar proses
pemilihan pelanggan berikutnya optimal, urutkan pelanggan berdasarkan waktu
pelayanan dalam urutan yang menaik.
· Jika pelanggan sudah terurut, kompleksitas
algoritma greedy = O(n).
·
Algoritma greedy untuk
penjadwalan pelanggan akan selalu menghasilkan solusi optimum.
·
Teorema. Jika t1 £ t2 £ … £ tn
maka pengurutan ij = j, 1 £
j £
n meminimumkan
untuk semua kemungkinan permutasi ij.
Referensi :
Referensi :










0 komentar:
Posting Komentar