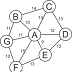
1. Vertex (simpul / node)
Sebuah graph dibentuk dari kumpulan titik yang dihubungkan dengan garis-garis. Titik-titik tersebut disebut vertex.
2. Edge (busur)
Merupakan garis penghubung antara dua vertex.
3. Adjacent (bertetangga)
Pada graph tak berarah (indirected graph) dua buah vertex / vertex disebut adjacent jika ada edge yang menghubungkan dua buah vertex. Sedangkan pada graph berarah (directed graph) sebuah vertex a disebut adjacent dengan vertex b jika ada vertex dari b ke a.
4. Weight
Apabila setiap edge mempunyai sebuah nilai (dapat berupa jarak, waktu atau biaya) yang menyatakan hubungan antara kedua buah vertex maka edge tersebut dikatakan memiliki bobot. Graph yang memiliki bobot dapat disebut sebagai graph berbobot atau weighted graph.
5. Path (lintasan)
Path adalah serangkaian vertex yang berbeda yang adjacent secara berturut turut dari vertex satu ke vertex berikutnya.
6. Direct (arah)
Merupakan arah suatu graph. Pada graph berarah (directed graph atau digraph) urutan vertex memiliki arti.
REPRESENTASI GRAPH
Dalam bidang ilmu komputer, sebuah graph dapat dinyatakan sebagai sebuah struktur data, atau secara spesifik dinamakan sebagai ADT(abstract data type) yang terdiri dari kumpulan vertex dan sisi yang membangun hubungan antar vertex. Konsep ADT graph ini merupakan turunan konsep graph dari bidang kajian matematika. Graph menampilkan visualisasi data dan hubungannya. Sedangkan jika berbicara masalah implementasi struktur data graph itu sendiri, isu utama yang dihadapi adalah bagaimana informasi itu disimpan dan dapat diakses dengan baik, ini yang dapat disebut dengan representasi internal. Secara umum terdapat dua macam representasi dari struktur data graph yang dapat diimplementasi. Pertama disebut adjacency list, dan diimplementasi dengan menampilkan masing-masing vertex sebagai sebuah struktur data yang mengandung senarai dari semua vertex yang saling berhubungan. Yang kedua adalah representasi berupa adjacency matrix di mana baris dan kolom dari matriks (jika dalam konteks implementasi berupa senarai dua dimensi) tersebut merepresentasikan vertex awal dan vertex tujuan dan sebuah entri di dalam senarai yang menyatakan apakah terdapat sisi di antara kedua vertex tersebut.
A. Adjacency list
Dalam teori graph, adjacency list merupakan bentuk representasi dari seluruh sisi atau edge dalam suatu graph sebagai suatu senarai. Vertex-vertex yang dihubungkan sisi atau edge tersebut dinyatakan sebagai vertex yang saling terkait. Dalam implementasinya, hash table digunakan untuk menghubungkan sebuah vertex dengan senarai berisi vertex-vertex yang saling terkait tersebut. Salah satu kekurangan dari teknik representasi ini adalah tidak adanya tempat untuk menyimpan nilai yang melekat pada sisi. Contoh nilai ini antara lain berupa jarak vertex, atau beban vertex.
/*------ADJACENCY LIST--------*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
struct edge {
int state;
char *name;
edge *next;
};
struct node {
char *name;
node *next;
edge *edge;
};
node *first=NULL;
int findNode(const node *temp, const char *name){
int status = false;
do{
if(strcmp(node->name, name)==0) status = true;
else {
node = node->next;
status = false;
}
}while(node != NULL || status != true);
return status;
}
void addNode(const char *name){
node *temp = first;
int status;
if(!temp){
temp = (node*)malloc(sizeof(node));
temp->name = (char*)malloc(sizeof(char)*strlen(name)=1);
strcpy(temp->name, name);
temp->edge = temp->next = NULL;
}
else{
status = findNode();
if(status == true) printf("Error. Node already exist\n");
}
first = temp;
}
void showNodes(){
node *temp = first;
if(!temp) return;
while(temp != NULL){
printf("%s\n", temp->name);
temp = temp->next;
}
}
//fungsi utama
main(){
addNode("A");
addNode("B");
addNode("C");
showNodes();
return 0;
}
B. Adjacency matrix
Adjacency Matrix merupakan representasi matriks nxn yang menyatakan hubungan antar vertex dalam suatu graph. Kolom dan baris dari matriks ini merepresentasikan vertex-vertex, dan nilai entri dalam matriks ini menyatakan hubungan antar vertex, apakah terdapat sisi yang menghubungkan kedua vertex tersebut.Pada sebuah matriks nxn, entri non-diagonal aij merepresentasikan sisi dari vertex i dan vertex j. Sedangkan entri diagonal aii menyatakan sisiKelebihan dari adjacency matrix ini adalah elemen matriksnya dapat diakses langsung melalui indeks, dengan begitu hubungan ketetanggan antara kedua vertex dapat ditentukan dengan langsung. Sedangkan kekurangan pada representasi ini adalah bila graph memiliki jumlah sisi atau edge yang relative sedikit, karena matriksnya bersifat jarang yaitu hanya mengandung elemen bukan nol yang sedikit. Kasus seperti ini merugikan, karena kebutuhan ruang memori untuk matriks menjadi boros dan tidak efisien karena komputer menyimpan elemen 0 yang tidak perlu.
/*------ADJACENCY MATRIX--------*/
#include <stdio.h>
struct node {
int info;
node *left, *right;
};
main(){
int A[5][5] = {0,5,0,2,0, 6,0,3,0,0, 0,0,0,0,9, 0,0,12,0,7, 0,14,0,0,0};
char nama[5] = "ABCDE";
node *point[5];
//simpul vertex pertama
node *P=newSimpul;
P->info = nama[0];
node *first = P;
node *last = P;
P->left = P->right = NULL;
point[0] = P;
printf("%c alamat %d ", P->info, point[0]);
//simpul vertex berikutnya
for(int i=1; i<=4; i++){
P = newSimpul;
P->info = nama[i];
last->left = P;
last = last->left;
P->left = P->right = NULL;
point[i] = P;
printf("\n%c alamat %d ", P->info, point[i]);
}
//simpul edge untuk semua vertex
node *Q = first;
for(int i=0; i<=4; i++){
node *R = Q;
printf("vertex %c --> ", Q->info);
for(int j=0; j<=4; j++){
if(A[i][j] != 0){
P = newSimpul;
P->info = A[i][j];
R->right = P;
P->left = point[j];
printf("berhubungan dengan %c, bobot %d", P->left->info, P->info);
P->right = NULL;
R = P;
}
}
printf("\n");
Q = Q->left;
}
}
SHORTEST PATH PROBLEM
Dalam teori graph masalah jalan terpendek adalah masalah menemukan jalan antara dua node (atau node) sedemikian rupa sehingga jumlah dari bobot dari ujung penyusunnya diminimalkan. Contohnya adalah menemukan cara tercepat untuk mendapatkan dari satu lokasi ke lokasi lain pada peta jalan, dalam hal ini merupakan titik lokasi dan merupakan segmen tepi jalan dan ditimbang oleh waktu yang dibutuhkan untuk perjalanan segmen itu.
Secara formal, diberi tertimbang grafik (yaitu, satu set V vertices, sebuah E set ujungnya, dan sebuah fungsi bobot bernilai real f: E → R), dan satu v elemen V, mencari jalur P dari v ke 'V sehingga minimal di antara semua jalan yang menghubungkan v ke v '.
Masalahnya juga terkadang disebut pasangan-tunggal masalah rute terpendek, untuk membedakannya dari generalisasi berikut:
Sumber-satu masalah shortest path, di mana kita harus menemukan jalan terpendek dari sumber node v ke semua node lainnya dalam grafik. Tujuan-tunggal masalah shortest path, di mana kita harus menemukan jalan terpendek dari semua titik dalam grafik ke sebuah node tujuan tunggal. Hal ini dapat dikurangi dengan sumber tunggal masalah jalan terpendek oleh membalik tepi dalam grafik. Semua pasangan masalah shortest path, di mana kita harus menemukan jalan terpendek antara setiap pasangan vertex v, v 'dalam grafik. Generalisasi ini memiliki algoritma secara signifikan lebih efisien dibandingkan dengan pendekatan sederhana menjalankan algoritma tunggal pasangan jalur terpendek pada semua pasangan vertex yang relevan.
Berikut merupakan beberapa contoh algoritma yang dapat digunakan untuk menyelesaikan masalah shortest path problem :
a. Algoritma dijkstra
Dinamai menurut penemunya, Edsger Dijkstra, adalah algoritma dengan prinsip greedy yang memecahkan masalah lintasan terpendek untuk sebuah graph berarah dengan bobot sisi yang tidak negatif.
Algoritma Dijkstra merupakan salah satu varian bentuk algoritma populer dalam pemecahan persoalan yang terkait dengan masalah optimasi. Sifatnya sederhana dan lempang (straightforward). Sesuai dengan arti greedy yang secara harafiah berarti tamak atau rakus – namun tidak dalam konteks negatif -, algoritma greedy ini hanya memikirkan solusi terbaik yang akan diambil pada setiap langkah tanpa memikirkan konsekuensi ke depan. Prinsipnya, ambillah apa yang bisa Anda dapatkan saat ini (take what you can get now!), dan keputusan yang telah diambil pada setiap langkah tidak akan bisa diubah kembali.
Elemen-elemen penyusun prinsip greedy pada Algoritma Dijkstra adalah :
1.Himpunan kandidat
Himpunan ini berisi elemen-elemen yang memiliki peluang untuk membentuk solusi. Pada persoalan lintasan terpendek dalam graph, himpunan kandidat ini adalah himpunan simpul pada graph tersebut.
2. Himpunan solusi
Himpunan ini berisi solusi dari permasalahan yang diselesaikan dan elemennya terdiri dari elemen dalam himpunan kandidat namun tidak semuanya atau dengan kata lain himpunan solusi ini adalah upabagian dari himpunan kandidat.
3. Fungsi seleksi
Fungsi seleksi adalah fungsi yang akan memilih setiap kandidat yang yang memungkinkan untuk menghasilkan solusi optimal pada setiap langkahnya.
4. Fungsi kelayakan
Fungsi kelayakan akan memeriksa apakah suatu kandidat yang telah terpilih (terseleksi) melanggar constraint atau tidak. Apabila kandidat melanggar constraint maka kandidat tidak akan dimasukkan ke dalam himpunan solusi.
5. Fungsi objektif
Fungsi objektif akan memaksimalkan atau meminimalkan nilai solusi. Tujuannya adalah memilih satu saja solusi terbaik dari masing-masing anggota himpunan solusi.
Ada beberapa kasus pencarian lintasan terpendek yang diselesaikan menggunakan algoritma Dijkstra, yaitu: pencarian lintasan terpendek antara dua buah simpul tertentu (a pair shortest path), pencarian lintasan terpendek antara semua pasangan simpul (all pairs shortest path), pencarian lintasan terpendek dari simpul tertentu ke semua simpul yang lain (single-source shortest path), serta pencarian lintasan terpendek antara dua buah simpul yang melalui beberapa simpul tertentu (intermediate shortest path).
b. Algoritma greedy
Adalah algoritma yang memecahkan masalah langkah demi langkah, pada setiap langkah:
1. Mengambil pilihan yang terbaik yang dapat diperoleh saat itu
2. Berharap bahwa dengan memilih optimum lokal pada setiap langkah akan mencapai optimum global. Algoritma greedy mengasumsikan bahwa optimum lokal merupakan bagian dari optimum global.
Prinsip algoritma greedy adalah: “take what you can get now!”. Ambil apa yang anda peroleh sekarang! Prinsip ini juga dipakai dalam pemecahan masalah optimasi. Dalam kehidupan sehari-hari, kita juga pernah menggunakan prinsip greedy, misalnya:
a. Memilih jurusan di Perguruan Tinggi
b. Memilih jalur tersingkat dari Bandung ke Jakarta.
c. Algoritma brute force
Adalah sebuah pendekatan yang ‘lempeng’ (straight forward) untuk memecahkan suatu masalah, biasanya didasarkan pada pernyataan masalah (problem statement) dan definisi konsep yang dilibatkan. Algoritma brute force memecahkan masalah dengan sangat sederhana, langsung dan dengan cara yang jelas (obvious way).
d. Algoritma heuristik
Adalah sebuah metode komputasi yang mengoptimalkan masalah dengan iteratif mencoba mengembangkan solusi kandidat berkaitan dengan suatu ukuran tertentu kualitas. Metaheuristics membuat sedikit atau tidak ada asumsi tentang masalah yang dioptimalkan dan dapat mencari ruang yang sangat besar solusi calon. Namun, metaheuristics tidak menjamin solusi optimal yang pernah ditemukan. istilah lain yang bermakna sama seperti metaheuristic, adalah: derivatif-bebas, cari langsung, hitam-kotak, atau bahkan hanya pengoptimasi heuristik.
Metaheuristics digunakan untuk optimasi kombinatorial yang merupakan solusi optimal dicari melalui ruang-pencarian diskrit. Contohnya adalah masalah salesman mana-ruang pencarian solusi calon tumbuh secara eksponensial sebagai ukuran meningkat masalah yang membuat pencarian yang melelahkan untuk solusi optimal layak. Fenomena ini dikenal sebagai kutukan dimensi. metaheuristics
e. Algoritma semut
Diperkenalkan oleh Moyson dan Manderick dan secara meluas dikembangkan oleh Marco Dorigo, merupakan teknik probabilistik untuk menyelesaikan masalah komputasi dengan menemukan jalur terbaik melalui grafik. Algoritma ini terinspirasi oleh perilaku semut dalam menemukan jalur dari koloninya menuju makanan.
f. Algorima A*
Dapat juga disebut sebagai Algoritma A Star, merupakan salah satu contoh algoritma pencarian yang cukup popular di dunia. Jika kita mengetikkan Algoritma A* pada sebuah mesin pencari, seperti google.com, maka akan kita temukan lebih dari sepuluh ribu literatur mengenai algoritma A* Beberapa terminologi dasar yang terdapat pada algoritma ini adalah starting point, simpul (nodes), A, open list, closed list, harga (cost), halangan (unwalkable). Starting point adalah sebuah terminologi untuk posisi awal sebuah benda. A adalah simpul yang sedang dijalankan dalam algortima pencarian jalan terpendek. Simpul adalah petak-petak kecil sebagai representasi dari area pathfinding. Bentuknya dapat berupa persegi, lingkaran, maupun segitiga. open list adalah tempat menyimpan data simpul yang mungkin diakses dari starting point maupun simpul yang sedang dijalankan. Closed list adalah tempat menyimpan data simpul sebelum A yang juga merupakan bagian dari jalur terpendek yang telah berhasil didapatkan. Harga (F) adalah nilai yang diperoleh dari penjumlahan nilai G, jumlah nilai tiap simpul dalam jalur terpendek dari starting point ke A, dan H, jumlah nilai perkiraan dari sebuah simpul ke simpul tujuan. Simpul tujuan yaitu simpul yang dituju. Rintangan adalah sebuah atribut yang menyatakan bahwa sebuah simpul tidak dapat dilalui oleh A.
Prinsip algoritma ini adalah mencari jalur terpendek dari sebuah simpul awal (starting point) menuju simpul tujuan dengan memperhatikan harga (F) terkecil.
ALGORITMA TRAVELLING SALESMAN PROBLEM (TSP)
Perjalanan The Salesman Problem (TSP)) merupakan masalah di optimasi kombinatorial dipelajari dalam riset operasi dan ilmu komputer teoritis. Mengingat daftar kota dan jarak berpasangan mereka, tugas ini adalah untuk menemukan sesingkat mungkin tur yang dilihat setiap kota tepat satu kali.
Masalahnya adalah pertama kali dirumuskan sebagai masalah matematika pada tahun 1930 dan merupakan salah satu masalah yang paling intensif dipelajari di optimasi. Ini digunakan sebagai patokan untuk metode optimasi banyak. Meskipun masalahnya adalah komputasi sulit, sejumlah besar metode heuristik dan tepat diketahui, sehingga beberapa hal dengan puluhan ribu kota dapat diselesaikan.
TSP memiliki beberapa aplikasi bahkan dalam perumusan yang paling murni, seperti perencanaan, logistik, dan pembuatan microchip. Sedikit diubah, tampak sebagai masalah-sub di banyak bidang, seperti sekuensing DNA. Dalam aplikasi ini, kota merupakan konsep, misalnya, pelanggan, poin menyolder, atau fragmen DNA, dan merupakan konsep jarak perjalanan kali atau biaya, atau mengukur kesamaan antara fragmen DNA. Pada banyak aplikasi, kendala sumber daya tambahan seperti jendela terbatas waktu atau membuat masalah jauh lebih sulit.
Dalam teori kompleksitas komputasi, versi keputusan TSP termasuk kelas masalah NP-lengkap. Jadi, diasumsikan bahwa tidak ada algoritma efisien untuk memecahkan TSPS. Dengan kata lain, kemungkinan besar kasus terburuk berjalan waktu untuk algoritma TSP meningkat secara eksponensial dengan jumlah kota, bahkan beberapa kasus dengan ratusan kota hanya akan mengambil banyak CPU tahun untuk menyelesaikan tepat.
ALGORITMA CHINESE POSTMAN PROBLEM (CPP)
Tugas seorang tukang pos adalah mengambil surat2 dari kantor pos dan mengirimkannya ke mesing2 alamat. Rata2 tukang pos akan melalui setiap jalan dalam wilayah kerjanya minimal satu kali. Permasalahannya adalah bagaimana tukang pos dapat merancang rute minimal agar pekerjaannya dapat terlaksana secara efisien.
Dalam teori graph, pewarnaan grafik adalah kasus khusus dari grafik pelabelan; itu adalah tugas dari label tradisional disebut "warna" untuk unsur-unsur subjek grafik untuk kendala tertentu. Dalam bentuk yang paling sederhana, ini adalah cara untuk mewarnai titik dari grafik tersebut bahwa tidak ada dua sudut yang berdekatan berbagi warna yang sama, ini disebut pewarnaan titik. Demikian pula, pewarnaan tepi memberikan warna untuk setiap sisi sehingga tidak ada dua sisi yang berdekatan berbagi warna yang sama, dan menghadapi pewarnaan grafik planar memberikan warna untuk setiap muka atau wilayah sehingga tidak ada dua wajah saham yang memiliki batas yang sama warna.
Pewarnaan Vertex adalah titik awal subjek, dan masalah pewarna lainnya bisa diubah menjadi versi vertex. Sebagai contoh, sebuah sisi pewarnaan grafik adalah hanya sebuah node pewarnaan grafik garis, dan wajah pewarnaan grafik planar hanya pewarnaan titik planar yang ganda. Namun, masalah pewarnaan simpul non-sering dinyatakan dan belajar seperti. Itulah sebagian untuk perspektif, dan sebagian lagi karena beberapa masalah yang terbaik dipelajari dalam bentuk non-titik, seperti misalnya adalah mewarnai tepi. Konvensi menggunakan warna berasal dari negara-negara mewarnai peta, di mana setiap wajah berwarna harfiah. Ini umum untuk mewarnai wajah grafik tertanam di pesawat. Dengan dualitas planar menjadi mewarnai simpul, dan dalam bentuk ini generalizes untuk semua grafik. Dalam matematika dan representasi komputer ini khas untuk menggunakan bilangan bulat positif atau nonnegatif pertama beberapa sebagai "warna". Secara umum kita dapat menggunakan himpunan terhingga sebagai himpunan "warna". Sifat dari masalah pewarnaan tergantung pada jumlah warna tetapi tidak pada apa yang mereka.
ALGORITMA MINIMUM SPANNING TREE (MST)
Mengingat grafik, terhubung tidak diarahkan, pohon rentang dari graph yang merupakan graph yang pohon dan menghubungkan semua node bersama. Sebuah grafik tunggal dapat memiliki banyak pohon merentang yang berbeda. Kita juga dapat menetapkan bobot untuk setiap tepi, yang merupakan nomor mewakili cara yang tidak menguntungkan itu, dan menggunakan ini untuk menetapkan berat ke pohon rentang dengan menghitung jumlah bobot dari tepi di pohon rentang. Sebuah pohon rentang minimum (MST) atau berat pohon rentang minimum adalah pohon rentang kemudian dengan berat kurang dari atau sama dengan berat setiap pohon rentang lainnya. Secara umum, setiap grafik tidak diarahkan (tidak harus terhubung) memiliki hutan rentang minimum, yang merupakan kesatuan dari pohon rentang minimum untuk komponen yang terhubung tersebut.
Salah satu contoh akan menjadi perusahaan TV kabel memasang kabel ke lingkungan baru. Jika dibatasi untuk mengubur kabel hanya di sepanjang jalan tertentu, maka akan ada grafik yang mewakili yang poin dihubungkan oleh path. Beberapa path mungkin akan lebih mahal, karena mereka lebih lama, atau memerlukan kabel yang akan dikubur lebih dalam; jalur ini akan diwakili oleh tepi dengan bobot yang lebih besar. Sebuah pohon rentang untuk graph yang akan menjadi bagian dari path yang tidak memiliki siklus tapi masih terhubung ke setiap rumah. Mungkin ada beberapa pohon merentang mungkin. Sebuah pohon rentang minimum akan menjadi satu dengan total biaya terendah.
Graph problem: http://macherish.blogspot.co.id/2010/06/nah-kmaren-kan-saya-uda-posting.html






0 komentar:
Posting Komentar